Where The Conventional Model Fails And The New Model Succeeds
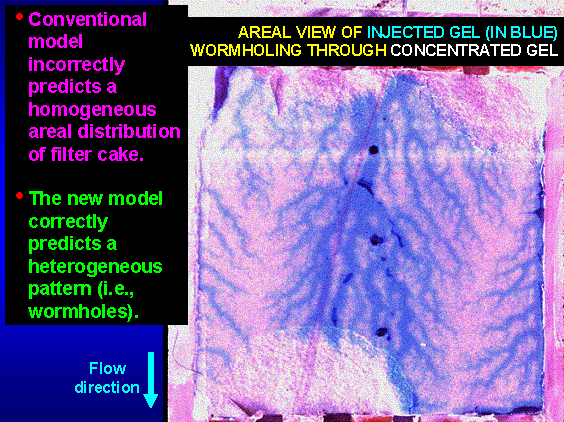
On first consideration, the behavior of leakoff versus time appears to support the conventional view of filter cake formation in hydraulic fractures (i.e., because leakoff varies with t-0.5). However, the conventional model assumed that a uniform filter cake formed. In contrast, our experiments revealed that fresh gel (containing 0.5% polymer) wormholed through concentrated gel (that contained, on average, 12 times the polymer concentration)—resulting in a distinctly non-uniform distribution of the filter cake on the fracture faces. Figure 1 above shows the wormhole pattern that developed during one experiment. (The dimensions of the fracture shown were Lf x hf x wf = 12x12x0.04 in.) Early in the process of gel injection, the wormhole pattern was very branched, with a significant fraction of the fracture area contacted by the wormholes. As additional gel volumes were injected, the wormholes became less branched, and a diminished fraction of the fracture area was contacted by the wormholes. This behavior was not surprising since the dehydrated gel became increasingly concentrated and less mobile and the mobility ratio (mobility of fresh gel divided by mobility of concentrated gel) increased with gel throughput.
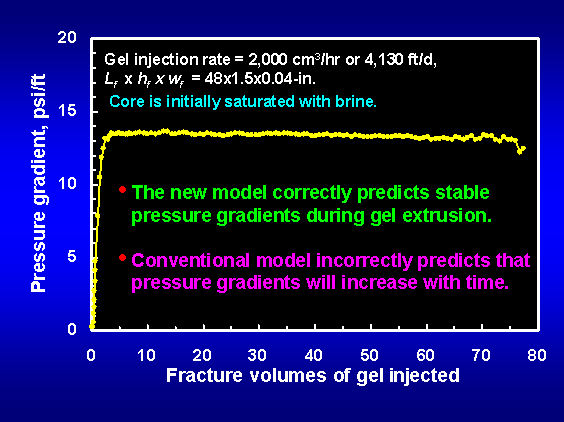
A second failure of the conventional filter cake model occurs with its prediction of pressure behavior versus gel throughput. In the conventional model, a single opening to flow exists that has a width that is equal to the fracture width minus twice the thickness of the filter cake at that point. The height of this opening is basically as high as the fracture. Thus, the flow opening is extremely high and narrow. The conventional model predicts that the filter cake on the fracture walls should uniformly increase in thickness with time—thereby decreasing the width of the active flow path in the fracture. Since the pressure gradient required for gel extrusion increases significantly with decreasing channel width, the conventional model predicts that the pressure gradients during gel extrusion should increase substantially with increased time and gel throughput. The figure below demonstrates that this prediction is incorrect—after gel breakthrough, pressure gradients are reasonably stable during gel extrusion.
In contrast, in the new model, for a given distance along the fracture, multiple flow channels exist (corresponding to the wormholes), the width of each channel could be only slightly less than the original fracture width, and the "height" of each channel is small compared to the total fracture height (but generally large compared to the fracture width). As mentioned above, the conventional model incorrectly predicts that the width of the active flow path in the fracture decreases with increasing gel throughput so that pressure gradients increase significantly with time. In contrast, in the new model, the width of the active flow path stays fairly constant with gel throughput and time, so the pressure gradient is independent of throughput and time—which is consistent with experimental observations (see figure below).