A New Model For Leakoff And Filter Cake Formation In Fractures
Recent observations inspired a new mechanistic model of gel propagation and dehydration in fractures. Consistent with our experimental results, this model assumed the following:
- Water can leave the gel and leak off through the fracture faces, but crosslinked polymer cannot.
- The mobile gel has the same composition as the injected gel.
- When an element of mobile gel dehydrates, that gel becomes immobile. For a given vicinity and time, t, in a fracture of width, wf, the average gel concentration (C/Co, which gives the gel concentration, C, relative to the concentration for the injected gel, Co) is:
C/Co = 1 +∫ul dt / wf
Eq. 1 where ul is the average leakoff rate for that vicinity. The process of transforming an element of mobile gel into concentrated, immobile gel may occur very rapidly. However, for the purposes of our model, this transition does not need to occur in zero time.
- At a given point along the fracture, the fracture surface is covered by either mobile gel (with fractional area, Am) or immobile gel (with fractional area, Ac) so that:
Am + Ac = 1
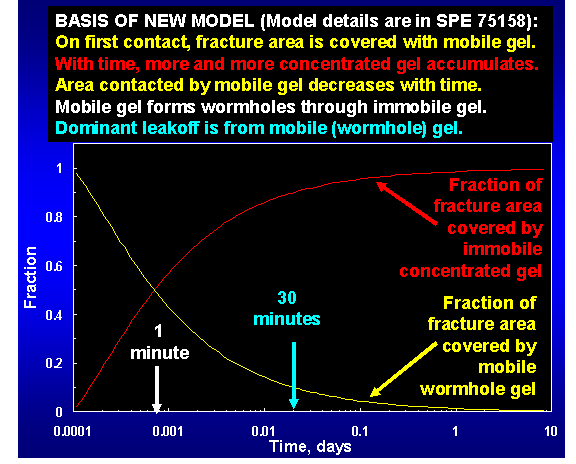
Eq. 2 The fraction of surface that contacts mobile gel decreases with time as more immobile gel forms (see above figure). Based on area and mass balances, the fractional area covered by concentrated gel at a given time and vicinity is approximated by:
Ac = [ C/Co– 1 ]/ [ C/Co ]Eq. 3 Presumably, as mobile gel in a wormhole dehydrates, a thin layer of concentrated gel forms at the fracture surface. However, this thin layer is continually pushed aside by the leakoff water or mobile gel, and the concentrated gel is added to the accumulation of immobile gel at the sides of the wormhole. Our model works reasonably well when the right side of Eq. 8 is taken to any power between 0.25 and 4.
- Water leakoff from immobile (dehydrated) gel (uc)
is negligible compared to that from the mobile gel (um). (The immobile gel continues to concentrate and lose water with time. However, this leakoff rate is small compared to that from the much more permeable mobile gel.)
um>> uc
Eq. 4 - The mobile gel has a finite permeability to water (kgel) that provides a fixed local leakoff flux (um) for the fracture surface that is in direct contact with mobile gel (i.e., the wormhole area that is in contact with the fracture faces).
ul≈ Am um
Eq. 5 Combining Eqs. 1 to 5 yields Eq. 6, which is the basis of the new model. The model predicts the leakoff rate (i.e., the rate of gel dehydration) at a given time and distance along the gel-contacted portion of a fracture.
ul = um / [1 + ∫ul dt /wf ]Eq. 6 The denominator of Eq. 6 reflects the rate of loss of fracture surface that is contacted by mobile gel (i.e., the wormhole-contact area). For our 24-hr-old Cr(III)-acetate-HPAM gel [0.5% Alcoflood 935, 0.0417% Cr(III) acetate], um has a value around 4 ft/d, which translates to a kgel value around 1 md. The latter value was confirmed from independent experiments. Calculations reveal that after 1 minute of gel contact, at least 50% of the fracture face is covered by concentrated gel rather than fresh gel (see figure above). Within 30 minutes of gel contact, more than 90% of the fracture face is covered by concentrated gel.
At a given distance along a fracture, the new model predicts that the wormhole area diminishes and the wormholes become more widely spaced with time. Consequently, one might expect pressure gradients to develop within the fracture transverse to the direction of flow. However, the compliant nature of the gel (even concentrated gel) mitigates the development of these transverse pressure gradients.