Model Differences

Although the predicted rate of leakoff versus time is about the same for both the new model and the conventional filtration model, the two models are basically different and predict different behavior for several important properties. In the conventional model, the thickness of the filter cake is areally uniform (at least locally); the entire fracture area continually experiences leakoff; and the leakoff rate decreases because of a steady growth in thickness of the filter cake. In the new model, the filter cake is areally heterogeneous; leakoff is significant only on the fracture area that is contacted by wormholes; and the global leakoff rate decreases because of a continual loss of fracture area that is contacted by wormholes. Our observations of wormhole behavior during gel extrusion through fractures are consistent with the new model, but inconsistent with the conventional filter cake model.
In the conventional model (left side of Figure 1 below), a single opening to flow exists that has a width that is equal to the fracture width minus twice the thickness of the filter cake at that point. The height of this opening is basically as high as the fracture. Thus, the flow opening is extremely high and narrow. In contrast, in the new model (right side of the figure below), for a given distance along the fracture, multiple flow channels exist (corresponding to the wormholes), the width of each channel could be only slightly less than the original fracture width, and the "height" of each channel is small compared to the total fracture height (but generally large compared to the fracture width). The conventional model incorrectly predicts that the width of the active flow path in the fracture decreases with increasing gel throughput (left side of the figure below) so that pressure gradients increase significantly with time. In contrast, in the new model, the width of the active flow path stays fairly constant with gel throughput and time (right side of the figure below), so the pressure gradient is independent of throughput and time—which is consistent with experimental observations.
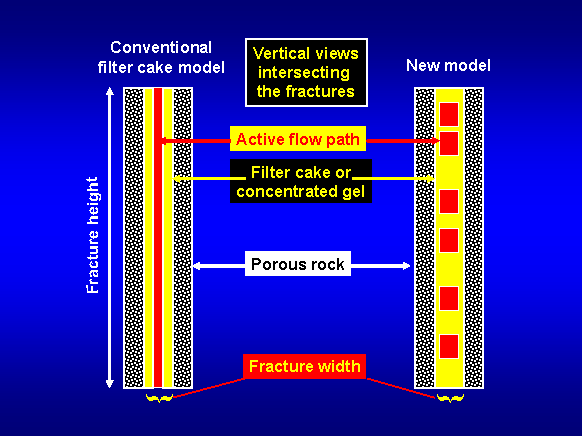
The two models predict significantly different flow and leakoff patterns and shear rates and stress levels within a fracture. These differences have important consequences for erosion of the filter cake, propagation of gels and particulates along fractures, transmission of pressures along fractures, fracture extension, and gel washout after placement. For a fixed pressure gradient, the new model predicts higher shear rates and shear stresses at the wall and much higher average fluid velocities than the conventional model. Consequently, greater erosion of the filter cake is predicted in the new model than in the conventional model.
Of course, the pressure gradient along the fracture impacts gel propagation and gel washout in water-shutoff treatments and fracture extension in hydraulic fracturing and produced water re-injection (i.e., by affecting the pressure at the fracture tip).