Conventional Filter Cake Model
In the conventional view of hydraulic fracturing, the rate of leakoff is determined by one (or a combination) of three mechanisms:
- Reservoir fluid viscosity/compressibility effects
- And the formation of a filter cake associated with particulate matter that was suspended in the fracturing fluid.
The widely accepted model of filter cake formation was introduced by Carter. Assume that a particulate-laden fluid (in blue above) contacts a rock interface (i.e., a fracture face, in red above) and a pressure difference, Δp, exists between the fracture and the porous rock. As solvent (with viscosity, μ) flows into the porous rock (black and white pattern above) at a velocity, ul, the particulates form a filter cake (in yellow above) of permeability, k, and thickness, L. At any given time, the filtrate velocity (i.e., the leakoff rate) is given by the Darcy equation.
The thickness of an incompressible filter cake grows at a rate that is proportional to the throughput of filtrate:
where a indicates the factor by which the particulates are concentrated during the transition from the suspension to the filter cake. Combining Eqs. 1 and 2 yields Eq. 3.
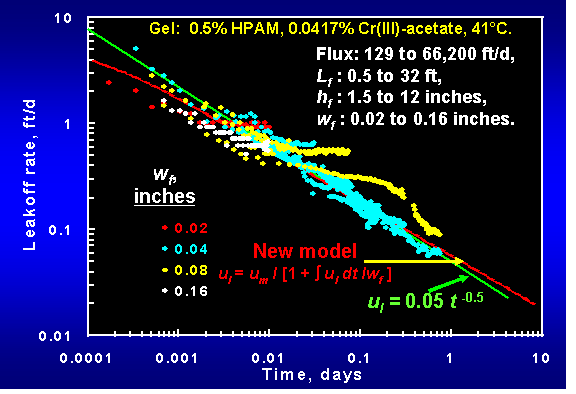
Eq. 4 presents a solution to Eq. 3.
where texp is the time of first exposure to filter cake for the element of fracture face of interest. The key result in Eq. 4 is that the leakoff rate is proportional to t-0.5. This proportionality was often verified experimentally—especially during static filtration experiments. An important assumption in the development of Eq. 4 was that the thickness of the filter cake was uniform at any given time. However, this assumption does not appear to be correct.