Can Gravity and Fluid Density Differences Be Exploited to Optimize Gelant Placement?
(Yes, for some cases in fractured wells. Usually, no, for unfractured wells.)
For most commercial gel treatments, the process of gel placement consists of two stages. First, the gelant is injected in a fluid form. Second, the well is shut in to allow gelation to take place. During the first stage in fractured wells, viscous forces virtually always dominate over gravity forces—that is, the gravity number is much less than one. To demonstrate, first consider a fracture with an effective permeability of 100 darcys, fluids with a density difference of 0.2 g/cm3, a viscosity of 1 cp, and sin Θ = 1 (i.e., the fracture is vertical). The dimensionless gravity number, G, provides a means to compare the importance of gravity forces relative to viscous forces during a displacement of oil by water.64
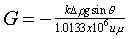
Gel Placement in Fractured Wells
For gel treatments in fractured production wells, gelant injection rates are typically very high—e.g., 50 to 500 BPD/ft of pay.10 Thus, for a fracture with a width of 0.01 ft, the velocity in the fracture during gelant injection typically ranges from 28,000 to 280,000 ft/d (10 to 100 cm/s). With these velocities, the G values range from 0.000193 to 0.00193. Note that the gravity number is substantially less than one. Even if the fracture was 100 times more permeable, the G values would still be much less than one. Thus, viscous forces dominate over gravity forces during gelant or gel injection into fractures. Therefore, the position of the gelant or gel front will not be significantly affected by gravity during injection.
When the well is shut in after gelant injection, how rapidly will gravity equilibrate the level of the gelant-oil interface in the fracture? If gravity alone acts as the driving force, then the vertical superficial velocity, uz, is given by Eq. 10.64
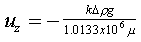
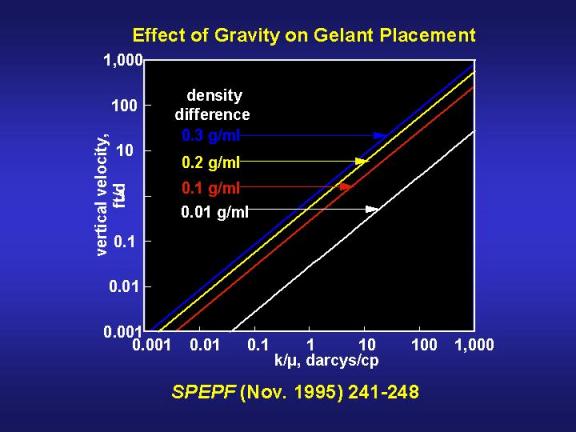
Fig. 22 illustrates uz as a function of k/µ and Δρ. Assume that oil has ready access to the fracture, either from the porous rock or from portions of the fracture beyond the gelant front. (This assumption will generally be valid for applications in production wells but not in injection wells unless oil is also injected.) Also assume that fluid displacements are piston-like (i.e., that capillary-pressure and relative-permeability effects are negligible). Given a fracture permeability of 100 darcys, a density difference of 0.2 g/cm3, and a 1-cp fluid viscosity, then uz is -55 ft/d. Thus, the rate of interface equilibration in a fracture can be quite rapid. For example, a fracture 55 ft high could be drained of gelant in 1 day if the gelation time is long enough.
Gel Placement in Unfractured Wells
Next consider an unfractured production well with a matrix permeability of 1 darcy. For the same fluid properties used in the previous examples,
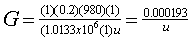
G will be less than 1 so long as u is greater than 0.000193 cm/s. If the gelant injection rate is 10 BPD/ft, then u > 0.000193 cm/s if the gelant is within a radius of 16.3 ft from the wellbore. Thus, during gelant injection in unfractured wells, viscous forces will dominate near the wellbore, but gravity becomes more important farther from the wellbore.
When the well is shut in after gelant injection, Eq. 10 can again be used to estimate the rate of settling for a gelant-oil interface. If k = 1 darcy, Δl= 0.2 g/cm3, and µ = 1 cp, then uz = -0.55 ft/d. Thus, even in a very permeable rock matrix, the rate of settling will be slow. The rate will be less in less-permeable rock or if a more viscous gelant is used. In concept, gravity could be exploited during gelant placement if the offending channel or aquifer is located below oil-productive zones. However, in view of the slow settling rate in porous rock, relatively long gelation times (weeks, at least) will be needed.
For applications in unfractured injection wells, slow settling rates and small density contrasts (between the gelant and the formation water) make gravity difficult to exploit during gelant placement.