In Unfractured Wells (Radial Flow), Is Protection of Oil Zones Needed During Gelant Placement in Heterogeneous Reservoirs?
(Yes.)

  1. PRRC Home
  2. Research Groups
  3. Reservoir Sweep Improvement
  4. Gel Placement Concepts
  5. Unfractured Wells

A common misconception is that protection of hydrocarbon productive zones is not needed during gelant placement if the reservoir is heterogeneous. For radial-flow systems, this concept can be easily disproved. Consider an unfractured water injection well in a reservoir (40-acre, 5-spot pattern, with unit mobility ratio) with seven non-communicating layers. The wellbore radius, rw, is 0.33 ft, and all layers have the same thickness. The permeabilities and porosities of the layers are listed in Table 1. The porosities (Ø, in percent) are related to permeabilities (k, in md) by Eq. 1.

Eq. 1

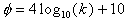
For this reservoir, the Dykstra-Parsons coefficient of permeability variation is approximately 0.9. This value indicates an extremely high degree of reservoir heterogeneity.2,3

A gelant is injected that has the same viscosity and mobility as water. For a given radius of penetration into the most-permeable layer, a gelant of this type penetrates the minimum distance into less-permeable zones.1,4Assume that the gelant is injected to reach a radius, rp1, of 50 ft in the most-permeable zone (Layer 1, or the 640-md layer). Zones are not isolated, so the gelant also penetrates into the other layers. Table 1 lists the radii of gelant penetration in the different layers (rpi). These values can be calculated easily using a simple form of the Darcy equation,1as given by Eq. 2.

Eq. 2

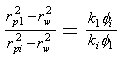
where the subscript, i, refers to a given less-permeable layer of interest. Note that the radius of gelant penetration into the 10-md layer is 7.7 ft. Thus, the gelant penetrates a significant distance into all layers, including the least-permeable layer

Table 1. For Radial Flow, Reservoir Heterogeneity Does Not Ensure an Effective Gel Placement Fraction of original injectivity retained
Layer k, md ø, % Radius of gelant penetration,ft Frr=2 Frr=10 Frr=100
1. 640 21.2 50.0 .75 .25 .029
2. 320 20.0 36.4 .76 .26 .031
3. 160 18.8 26.5 .77 .28 .033
4. 80 17.6 19.4 .79 .29 .036
5. 40 16.4 14.2 .80 .31 .039
6. 20 15.2 10.4 .81 .33 .042
7. 10 14.0 7.7 .83 .35 .046

After gelant injection, the well is shut in during gelation. After gelation, water injection is resumed. Wherever the gel forms, the permeability to water is reduced by the residual resistance factor, Frr. This causes some injectivity loss in all layers that contain gel. We are interested in the relative injectivity that is retained in each of the layers after the gel treatment, (i.e., final water injectivity divided by initial water injectivity). Table 1 lists these values for gel Frrvalues of 2, 10, and 100 (corresponding to weak, moderate, and strong gels, respectively). In all three cases, the gel treatment causes almost as much injectivity loss in the high-permeability zones as in the low-permeability zones. In other words, the gel treatment does not significantly improve the flow profile. In these examples, the residual resistance factor was assumed to be independent of permeability. For polymers and weak gels, residual resistance factors usually increase with decreasing permeability,5-9potentially leading to gel treatments that damage low-permeability zones more than high-permeability zones.

In summary, extreme reservoir heterogeneity does not eliminate the need to protect hydrocarbon-productive zones during gelant placement in unfractured injection wells (where flow is radial). A more detailed discussion of this point can be found in Ref. 2.